Systems of Linear Equations

Like our last topic, linear equations, systems of linear equations is something that’s likely already familiar to many of you, albeit perhaps distantly.

Definition

We form a linear system when we have multiple linear equations with the same unknowns. In the last section, we saw the example of the linear equation \(3x + 7 = 0\), and many of you surely noticed that this equation is only satisfied when \(x = -\frac{7}{3}\). When we combine equations to form a system, we say that the system is satisfied when all of its constituent equations are also satisfied.

Example

Let’s combine this example equation with another example from the previous section to form a system:

\[\begin{align*} 3x - y + 4 &= 0 \\ 3x + 7 &= 0 \end{align*}\]

By our definition, we have a solution to this system when both equations are simultaneously satisfied. We know that the second equation is only satisfied when \(x = -\frac{7}{3}\), so using this we can solve for the value of \(y\) necessary to satisfy the system using some algebra:

\[\begin{align*} 0 &= 3\left(-\frac{7}{3}\right) - y + 4 \\ y &= 3\left(-\frac{7}{3}\right) + 4 \\ y &= -7 + 4 \\ y &= -3 \end{align*}\]

Therefore, both equations (and therefore the system as a whole) are satisfied when \(x = -\frac{7}{3}\) and \(y = -3\).

This system of equations was likely much easier to solve than many of the systems typically solved by high schoolers. This comes from the fact that we could fairly easily obtain a numeric value for \(x\) and then use that value to obtain a value for \(y\). A system of equations like:

\[\begin{align*} 3x - y + 4 &= 0 \\ 3x + y - 3 &= 0 \\ \end{align*}\]

would require considerably more effort to solve. (I’ll leave it to you to take a crack at solving this one to demonstrate the amount of work needed to find the solution.) The goal of solving linear systems using the methods of linear algebra is to turn a system of equations like this hard example into a system of equations that’s more like the easy example.

Types of Solutions

When given a system of linear equations like this, the system will always fall into one of three cases:

• There are no solutions to the system of equations. For example, consider the system \(x + 1 = 0\) and \(x - 1 = 0\), which has no solutions.
• There is exactly one solution to the system of equations. Both of the examples above are of this type.
• The are infinitely many solutions to the system of equations. For example, consider the system \(0 = x - y + 1\) and \(0 = -x + y - 1\).

It must be emphasized that no matter what, if all the equations in the system meet our definition of linear from the previous section, then the system will always have 0, 1, or infinitely many solutions.

Intuition

The case of a one-variable system of linear equations is somewhat boring; all one-variable linear equations have one solution (e.g., \(x + 3 = 0\) is only solved by \(x = -3\)). So when you combine them into a system, either they both have the same one solution, or they have different solutions and it’s impossible to satisfy both simultaneously.

The case where you have a system of linear equations in two variables is where things can get to be a bit more interesting. Consider the following system of two linear equations:

\[\begin{align*} y &= -3x + 4 \\ y &= -x + 2 \end{align*}\]

These are linear equations because we can write them in terms of the definition given in the previous section. Writing them this way looks like:

\[\begin{align*} 0 &= -3x - y + 4 \\ 0 &= -x - y + 2 \end{align*}\]

However, writing them as an equation of one of the variables makes these equations much easier to plot, and this plot appears below:

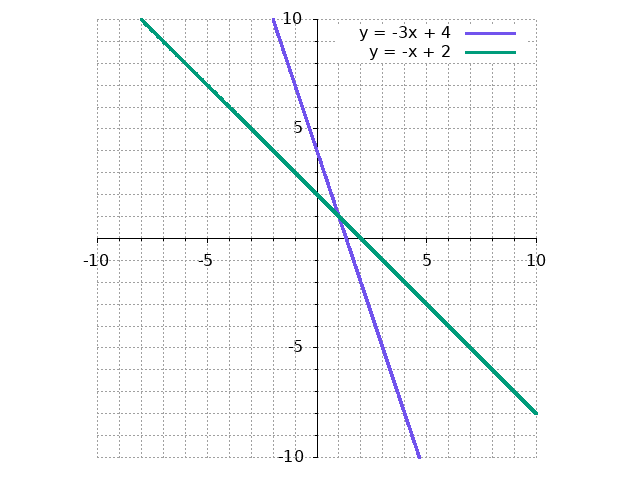
Now consider, for a moment, what each of these two lines represents. Specifically, let’s zoom in on the line \(y = -3x + 4\). Each point, \((x,y)\), on that line is only “on the line” if it satisfies the equation \(y = -3x + 4\) (or equivalently, \(0 = -3x - y + 4\)). Therefore, we can think of each line as the set of all solutions to one of the equations, and the point where these two lines cross is where both equations are satisfied simultaneously.

Thus, finding the “solution to the system,” which is equivalent to asking when both equations are satisfied, can be described visually as asking where the two lines intersect. This visual representation is helpful for understanding why we can get one of the three types of sets of solutions we talked about earlier. No solutions correspond to a system like this, where the lines are parallel:

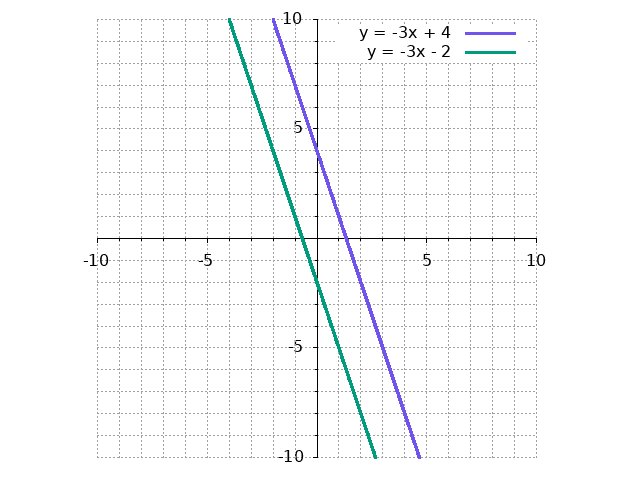
One solution corresponds to a case like above, where the two lines intersect at a single point. Infinitely many solutions corresponds to a case where you have all the lines in the system “laying on top of each other,” like so:

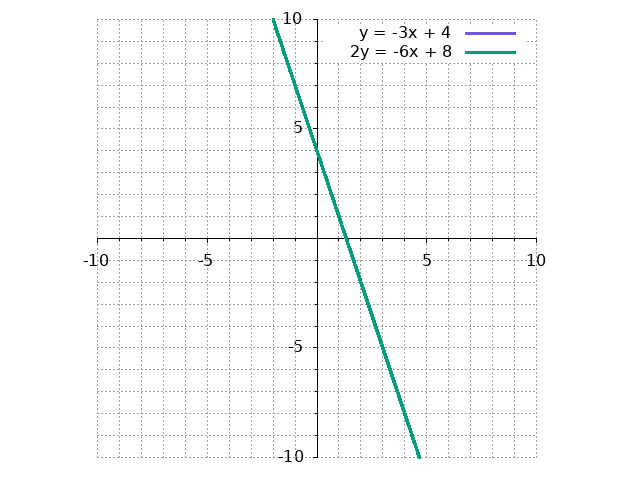
Hopefully this makes it clear why we couldn’t have a system of linear equations with exactly two solutions; in order for this to happen, one of the lines would have to “bend.” This is, of course, possible using non-linear equations, but for the purposes of linear algebra we don’t worry about those.

Higher Dimensions

All of this still applies to higher dimensions, although the visualization gets much messier. For three variables, this would correspond to a 3D graph. Each linear equation would create a plane rather than a line, so two planes could be parallel (resulting in no solutions) or intersect and create a line of shared solutions (infinitely many solutions). Once we add a third plane, all three planes can intersect at a single point, have no points where all three planes intersect, or the third plane can be right on top of one of the other two and not change the set of solutions.

This image from Wikipedia shows this case, the blue line is the intersection of two of the three planes, and all three intersect at a single common point.

By Alksentrs at en.wikipedia - Own work (Original text: Own work, based on en:Image:Linearsubspace.svg (by en:User:Jakob.scholbach).) Transferred from en.wikipedia to Commons by User:Ylebru using CommonsHelper., CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=5773029

---